Welcome to the second day! In today’s problem set, we will be exploring geometry! Angles, segments, polygons, circles, coordinates… Also, if you’ve solved some puzzles on day 1, we will release the solutions tonight!
By the way, today’s puzzle 3 is very fun! Even if you don’t want to solve it, I recommend that you read through it.
If you are able to solve any of the puzzles, submit your solution by Wednesday March 5, 11:25am to win a treat.
Puzzle 1 - Google Earth
In grade 9 geography classes (CGC1W), students are asked to explore the earth using Google Earth. Of course, one of the things they do is finding our school. They also use the ruler tool to measure the dimension of our school buildings.
The following is an approximation of the two buildings of Lisgar. Assuming that each little square of the grid is \(1 \times 1\), what’s the total area of these buildings?
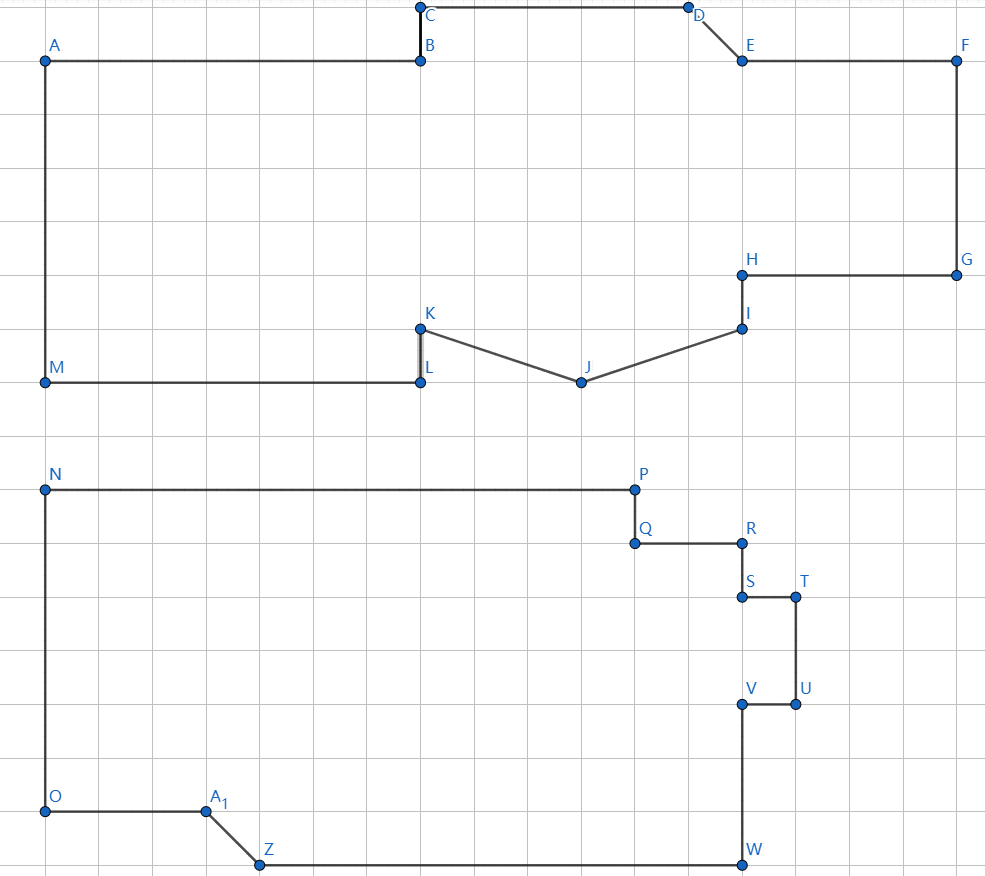
Clarification: once the diagram above contains thin grid lines that make it ambiguous what “little square” means. Now the diagram is accurate. Answers computed using the old ambiguous diagram will also be accepted as correct.
Puzzle 2 - Parabolic Ice Cream
I love ice creams. Today on my way home I saw an ice cream truck, and I decided that I had to stop and buy an ice cream cone.
After I got my ice cream cone, however, I feel that it’s a lot lighter than it looks. So I ate all the ice cream and took a look at the cone. I quickly realize that the inside of the cone is round and smooth while the outside is flat: that means the cone is hollow so that the ice cream man can save some ice cream!
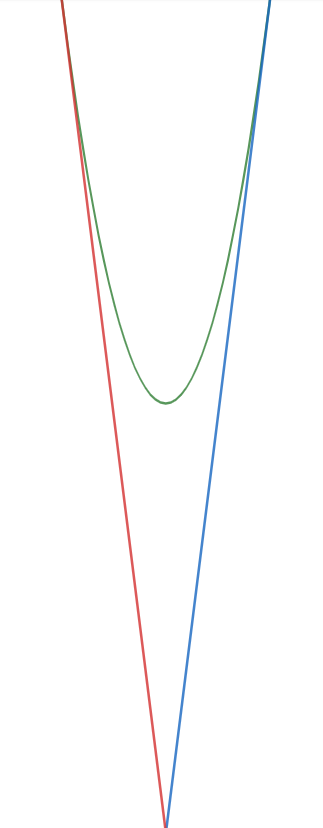
Since I was going to have my parabola quiz the next day, I was very sensitive to parabolas and figured out immediately that the inside of the cone is a parabola, if you look at the cross section after cutting it in the middle.
The inside of the ice cream cone has formula \(y = x^{2}\), and the tip of the cone is exactly \(16\) units below the lowest point of the parabola. If you draw the entire diagram of \(y = x^{2}\) out, the outside of the cone is just touching the parabola. Of course the ice cream can’t be infinitely high so it stops at where the inside and outside touch each other.
The outside of the cone is made up of two lines, as you can see in the diagram, what is the product of their slopes?
Puzzle 3 - Geometry Dash
Geometry Dash is a platformer game that has been famous among the computer science classes. It is so visually-appealing and fun to play that sometimes, people would rather play it during the Lisgar Computing Club meeting, instead of solving fun competitive programming problems!
In Geometry Dash, the player controls a cube that keeps advancing in an auto-scrolling map. The level restarts if the cube hits an obstacle. The player can press Space, which will cause the cube to jump.
Andre, co-head of the computing club, would like to show his friends how well he can play Geometry Dash. Unfortunately, his friend has even better skill than him! Andre then decided to surprise his friend by showing him that he can compute the area that the cube sweeps1 during its jump process.
The jump process can be modelled as follows: Since Geometry Dash is a 2D game, we will use 2D geometry only. The cube becomes a square of side length \(6\) in our model. Let’s assume that the center of the square is at coordinate \((0, 0)\) before it starts the jump process. During the jump process, the center of the square will rotate around point \((6, 0)\) clockwise for \(180^{\circ}\) (i.e. the process stops when the center reaches \((12, 0)\)). However, the square will stay still/unmoved relative to its center. Thus, during the jump process, the four sides of the square remain parallel to the x- or y-axis.
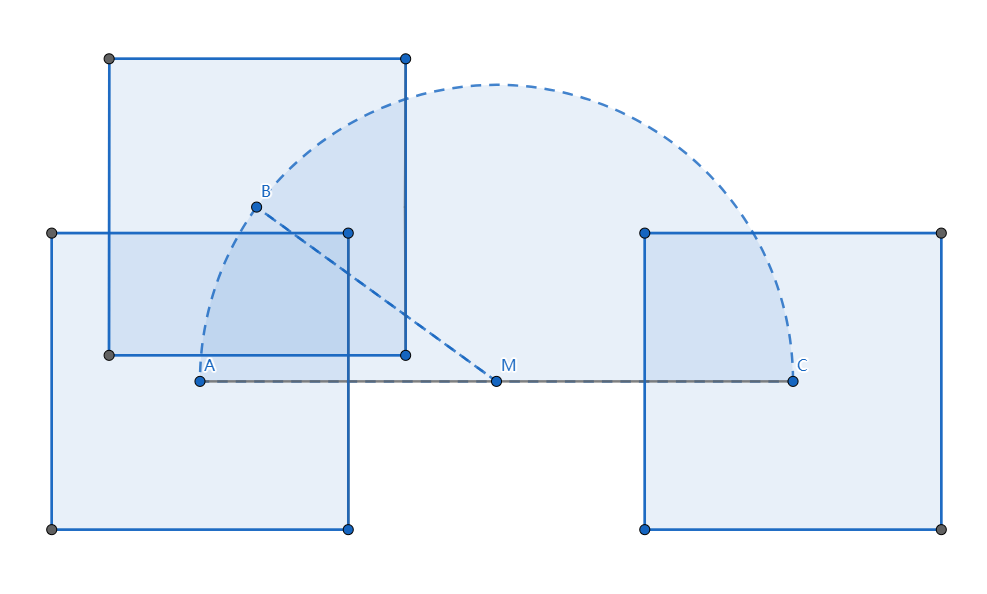
As depicted in the diagram: The square is initially centered at \(A(0, 0)\), then the center rotates around point \(M(6, 0)\), ending at \(C(12, 0)\). The diagram only shows one intermediate state, that is when the square is centered at \(B\). As you can see, the four sides of the square stay still relative to \(B\), as if the square is “copy-pasted” from \(A\) to \(B\).
Can you help Andre compute the area that the cube sweeps during this jump process?
-
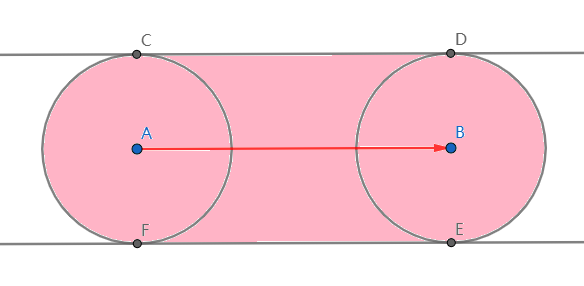
The area that a shape sweeps during its movement is defined as follows: if a point has ever been in the shape at any moment during the movement process, then that point counts towards the area that the shape sweeps. For example, in the diagram below, circle \(A\) moves in the direction of the arrow and ends at where circle \(B\) is. The shaded pink area is what circle \(A\) sweeps during this process.
 ↩︎
↩︎