The third day of our math week will be about combinatorics, a branch of mathematics useful especially in real life. It is all about probability and counting.
If you are able to solve any of the puzzles, submit your solution by Thursday March 6, 11:25am to win a treat! Additionally, the first solver of each problem gets a bonus! Check out the event planning page for more details.
Puzzle 1 - Loonies
One of the things that you often see in a combinatorics problem is coin flipping. In this problem, I got you five dollars. To be precise, five loonies. I’m going to flip them one by one in a fair way (chance of getting heads and tails are both \(50\%\)).
Subtask 1
Let H denote heads and let G denote GOOSE (tails). What’s the probability
that the outcomes of the flips are HGHHG, in that order?
Subtask 2
What is the chance of getting two consecutive geese? For example, GGHHH,
HGGHH and GGHGG all have two consecutive geese.
Extension
Note: this extension task is very fun to explore but quite hard to prove rigorously. We are not collecting responses for it. If you would like to discuss it with us, go to the Contact page.
Suppose, instead of H, we write the digit \(1\), and instead of G, we write
the digit \(2\). Also, we prepend our result with \(0.\), thus obtaining a real
number. For instance, GGHGG gives us the number \(0.22122\). The loonie is
flipped an infinite number of times. What is the probability that we obtain a
rational number?
Puzzle 2 - Bonbons
I’m really tired of chocolate bars recently. I walked into a chocolate shop and discovered a new type of fancy chocolate: bonbons.
They’re so fancy. According to Wikipedia,
(Bonbons) may contain brittle, nougat, dragée, or caramel. Other possible fillings include butterscotch, fondant, fudge, ganache, gianduja, marzipan, praline, and truffle.
(Quite a few words that I don’t know :)
This chocolate shop displays all their bonbons in a \(8 \times 8\) grid, meaning that they offer \(64\) different fillings! The downside of this is that since I am very indecisive, I have no idea what bonbons I should purchase. To make my life easier, I decided to choose just one rectangular region in the grid, and only grab the bonbons in that region.
For instance, if I only have a \(2 \times 2\) grid to choose from, then I have \(9\) possible choices:
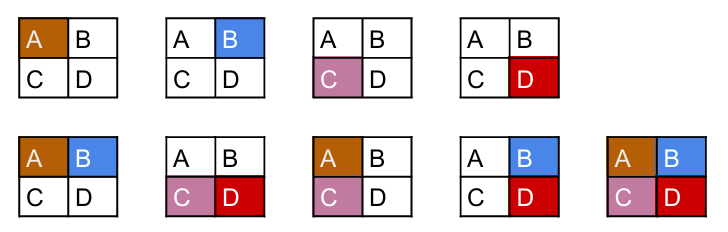
But now, how many choices do I have for the \(8 \times 8\) bonbon grid?
Puzzle 3 - Music Scheduling
We all know that Lisgar is a semestered school, which means that we have four courses in the first semester and four different courses in the second. However, a few other schools in the board (e.g. Merivale HS) are not. Instead, students take all eight courses throughout the whole year. On day ones and day twos people attend different classes.
Unfortunately, that means they also have to do eight exams in June! In order to
relieve students’ stress during the final exam week, the principal decided to
play relaxing music before each day’s exam. There are only three pieces to
choose from, denoted A, B and C. For some reason, song A and song B
can’t be arranged on two consecutive exam days. How many ways are there to
assign each exam day one piece of music, satisfying the constraint? (e.g.
CCBACAAC is not fine because B and A are next to each other, while
CBCACBCA is fine)